Dalam analisis rangkaian, rangkaian sederhana dapat dianalisis dengan menggunakan alat dasar analisa seperti hukum ohm, KVL dan KCL. Tapi untuk sirkuit kompleks yang terdiri dari berbagai sumber terkontrol, alat ini selain dengan seri dan paralel metode yang dapat diandalkan. Oleh karena itu, untuk menemukan variabel cabang di sirkuit tersebut, metode analisis nodal dan mesh (atau loop) yang digunakan. Dengan menggunakan metode klasik ini, variabel sirkuit seperti tegangan dan arus mudah ditentukan di cabang mana pun tanpa pusing – pusing lagi. Mari kita lihat secara detail tentang analisis mesh.
Analisis Mesh
Mesh adalah sebuah loop yang tidak terdiri dari apapun loop lain di dalamnya. Teknik analisis Mesh , menggunakan arus mesh sebagai variabel, bukan arus dalam elemen untuk menganalisis rangkaian. Oleh karena itu, metode ini benar-benar mengurangi jumlah persamaan harus dipecahkan. Analisis Mesh menerapkan Kirchhoff Voltage Law (KVL) untuk menentukan arus dikenal di sirkuit tertentu. Mesh analisis juga disebut sebagai metode jala-saat atau analisis lingkaran. Setelah menemukan arus jala menggunakan KVL, tegangan di mana saja di sirkuit tertentu dapat ditentukan dengan menggunakan hukum Ohm.
Langkah-langkah untuk Analisis teknik analisis jala
1) Periksa apakah ada kemungkinan untuk mengubah semua sumber arus di sirkuit yang diberikan kepada sumber tegangan.
2) Menetapkan arah saat ini untuk masing-masing jala dalam rangkaian tertentu dan mengikuti arah yang sama untuk setiap mesh.
3) Terapkan KVL untuk setiap mesh dan menyederhanakan persamaan KVL.
4) Memecahkan persamaan simultan berbagai jerat untuk mendapatkan arus mesh dan persamaan ini persis sama dengan jumlah jerat hadir dalam jaringan.
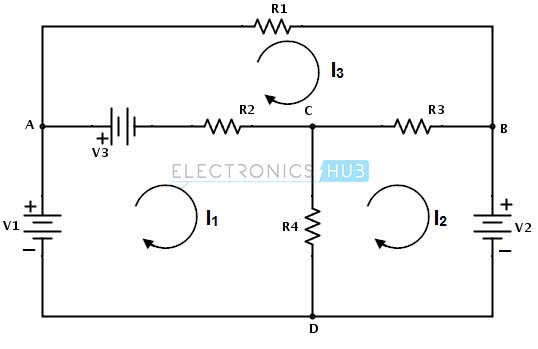
Pertimbangkan bawah sirkuit DC untuk menerapkan analisis saat mesh, sehingga arus di jerat yang berbeda dapat ditemukan. Pada gambar di bawah ini ada tiga jerat hadir sebagai Acda, CBDC dan ABCA tapi jalan ABDA tidak mesh. Sebagai langkah pertama, arus yang melalui masing-masing jala ditugaskan dengan arah yang sama seperti yang ditunjukkan pada gambar.
Kedua, untuk setiap mesh kita harus menerapkan KVL. Dengan menerapkan KVL sekitar loop pertama atau mesh kita temukan
V1 – V3 – R2 (I1 – I 3) – R4 (I1 – I 2) = 0
V1 – V3 = I1 (R2 + R4) – I2R4 – I3R2 ……………… (1)
Demikian pula, dengan menerapkan KVL sekitar mesh kedua ,
-V2 – R3 (I 2 – I 3) – R4 (I 2 – I1) = 0
– V2 = – I1R4 + I 2 (R3 + R4) – I 3 R3 ……………………… (2)
Dan dengan menerapkan KVL sekitar mesh ketiga atau loop yang yang ditemukan,
V3 – R1I 3 – R3 (I 3 – I 2) – R2 (I 3 – I1) = 0
V3 = – I1R2 – I2R3 + I3 (R1 + R2 + R3) ……………………… (3)
Oleh karena itu, dengan memecahkan di atas tiga persamaan kita bisa mendapatkan arus mesh untuk setiap mesh di sirkuit yang diberikan.
Contoh soal analisis mesh:
Contoh 1:
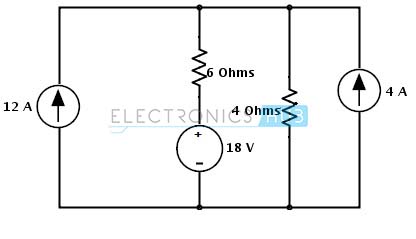
Perhatikan contoh berikut ini di mana kita menemukan tegangan sumber arus 12A menggunakan analisis mesh.Dalam rangkaian diberikan semua sumber adalah sumber arus.
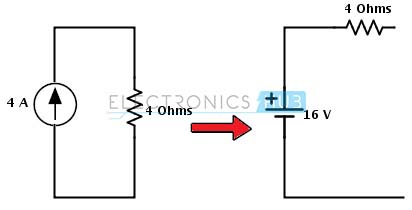
Langkah 1: Dalam rangkaian ada kemungkinan untuk mengubah sumber arus ke sumber tegangan pada tangan kanan sisi sumber dengan resistansi paralel. Sumber arus diubah menjadi sumber tegangan dengan menempatkan nilai yang sama resistor secara seri dengan sumber tegangan dan tegangan dalam sumber yang ditentukan sebagai
Vs = Is Rs
= 4 × 4 = 16 Volt
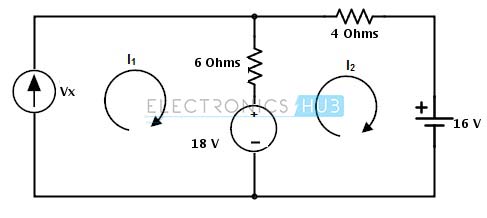
Langkah 2: Menetapkan arus cabang sebagai I1 dan I2 ke cabang masing-masing atau loop dan mewakili arah arus seperti yang ditunjukkan di bawah ini.
Langkah 3: Terapkan KVL untuk setiap jala di sirkuit yang diberikan
Mesh -1:
Vx – 6 × (I1 – I 2) – 18 = 0
Mengganti I1 = 12 A
Vx + 6I2 = 90 …………………… (1)
Mesh – 2:
18-6 × (I 2 – I1) – 4 × I 2-16 = 0
2 – 10 × I2 + 6 (12) = 0
I2 = 74/10
= 7,4 Amps
Mengganti dalam persamaan 1 kita mendapatkan
Vx = 90-44,4
= 45,6 Volt
Contoh 2:
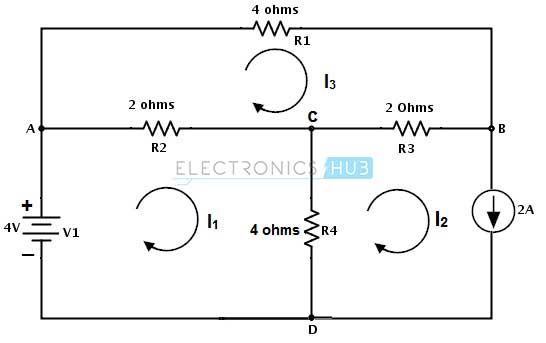
Pertimbangkan bawah sirkuit di mana kita menentukan tegangan sumber arus dan cabang Iac saat ini.Menetapkan arah seperti yang ditunjukkan di bawah ini dan perhatikan bahwa saat ini ditugaskan berlawanan dengan arus sumber di lingkaran kedua.
Dengan menerapkan KVL untuk mesh pertama kita mendapatkan
Dengan menerapkan KVL untuk mesh pertama kita mendapatkan
V1 – R2 (I1 – I 3) – R4 (I1 – I 2) = 0
4 – 2 I1 – 2I3 – 4I1 – 4I2 = 0
-6I1 – 2I3 = 4 …………… (1)
Dengan menerapkan KVL untuk mesh kedua kami mendapatkan
-Vc – R4 (I 2 – I1) – R3 (I 2 – I 3) = 0
– Vc = 4I2 – 4I1 + 2I2 – 2I3 = 0
– Vc = – 4I1 + 6I2 – 2I3
Tapi I2 = -2 A, maka
– Vc = – 4I1 – 12-2 I3 ………………… (2).
Dengan menerapkan KVL untuk mesh ketiga kita
– R1 I 3 – R3 (I 3 – I 2) – R2 (I 3 – I1) = 0
-4 I3 – 2I3 + 2I2 – 2I3 + 2I1 = 0
– 8I3 – 4 + 2I1 = 0 (dengan menggantikan I2 = -2 A)
2I1 – 8I3 = 4 ………………… (3)
Dengan memecahkan 1 dan 3 persamaan kita mendapatkan I3 = -0,615 dan I1 = 4,46
Oleh karena itu, tegangan Vc = 4 (4,46) + 12 + 2 (-0,615)
Vc = 28,61 V
Dan Iac cabang arus = I1- I3
Iac = 5,075 amp
Demikian juga kita dapat menemukan setiap saat cabang menggunakan analisis mesh.
Super Analisis Mesh
Seperti kita lihat pada contoh 2, mengandung sumber arus di salah satu cabang. Dan sebelum penerapan analisis mesh sirkuit itu, kita mengasumsikan tegangan yang tidak diketahui di sumber arus dan kemudian jala analisis diterapkan. Ini adalah pendekatan yang cukup sulit dan ini bisa diatasi dengan menerapkan teknik supermesh.
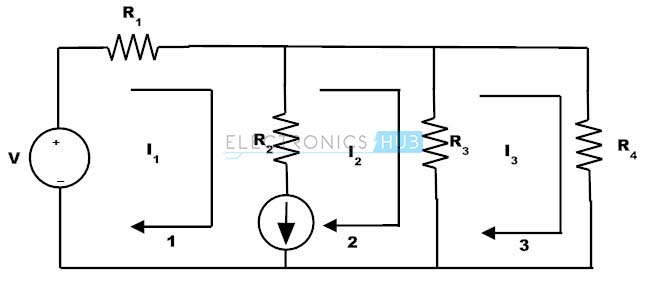
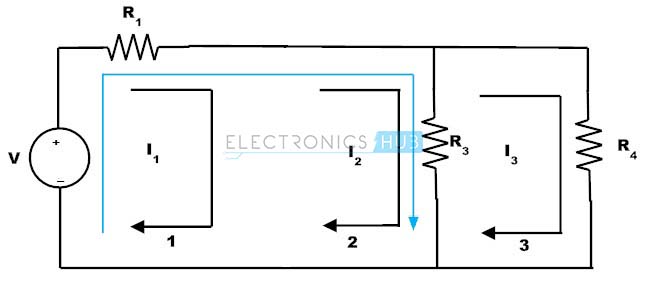
Super mesh terbentuk ketika dua jerat berdekatan berbagi sumber arus umum dan tidak satupun dari (berdekatan) jerat mengandung sumber arus dalam loop luar. Pertimbangkan sirkuit di bawah ini di mana Super mesh dibentuk oleh lingkaran di sekitar sumber arus.
Sumber arus umum untuk jerat 1 dan 2 dan karena itu harus dianalisa secara independen. Untuk mencapai hal ini, menganggap cabang yang berisi sumber arus terbuka hubung dan membuat jala baru yang disebut Super mesh.
Menulis KVL super mesh kita
V = I1R1 + (I2 – I3) R3
= I1R1 + I2R3 – I3R3
Menerapkan KVL ke Mesh 3 kita
(I3 – I2) R3 + I3R4 = 0
Dan perbedaan antara dua arus jala memberikan arus dari sumber arus. Berikut arah sumber arus dalam loop arus arah I1. Oleh karena itu I1 lebih dari I2, maka
I = I1 – I2
Jadi, dengan menggunakan tiga persamaan ini jala kita dapat dengan mudah menemukan tiga arus yang tidak diketahui dalam jaringan.
Contoh analisis supermesh
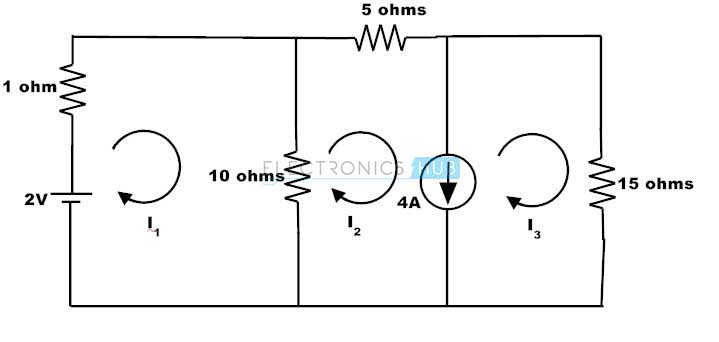
Perhatikan contoh berikut ini di mana kita harus menemukan arus melalui 10 ohm resistor.
Dengan menerapkan KVL ke jala 1 kita mendapatkan
1I1 + 10 (I1 – I2) = 2
11I1 – 10 I2 = 2 …………………………. (1)
Jerat 2 dan 3 terdiri dari 4A sumber arus dan karenanya membentuk mesh yang super. Arus dari sumber arus 4A adalah arah I3 dan dengan demikian super jala saat diberikan sebagai
I = I3 – I2
I3 – I2 = 4 …………………………. (2)
Dengan menerapkan KVL untuk loop luar super jala kita,
– 10 (I2 – I1) – 5I2 – 15I3 = 0
10I1 – 15I2 – 15I3 = 0 …………………… .. (3)
Dengan memecahkan 1, 2 dan 3 persamaan, kita mendapatkan
I1 = -2,35 A
I2 = -2,78 A
I3 = 1,22 A
Oleh karena itu arus melalui 10 ohm resistor I1 – I2
= -2,35 + 2,78 A
= 0,43 A
sumber http://www.electronicshub.org/mesh-analysis/